Notes of 推荐系统公开课 by Shusen Wang

Disclaimer: The content herein is sourced from Shusen Wang’s YouTube Channel, specifically the Playlist titled Recommendation System. This post is intended for personal study purposes.

1 概要
2 召回
3 排序
4 特征交叉
5 行为序列
7 物品冷启
8 涨指标的方法

概要

概要01 推荐系统的基本概念

转化流程

曝光（Impression） --> 点击（Click） --> 滑动到底(ScrowToEnd), 点赞(Like), 收藏(Collect), 转发(Share) --> 评论(Comment)

（短期）消费指标：

• 点击率 = 点击次数 / 曝光次数
• 点赞率 = 点赞次数 / 点击次数
• 收藏率 = 收藏次数 / 点击次数
• 转发率 = 转发次数 / 点击次数
• 阅读完成率 = 滑动到底次数 / 点击次数 $\times f$(笔记长度)

虽然点击率是重要的优化指标，但不能是唯一的指标，否则骗点击的标题就会泛滥。其他指标也可以反映出用户对笔记的兴趣。 $f$(笔记长度) 是一个归一化的函数，这是因为笔记越长，完成阅读的比例就越低。如果没有这个归一化的函数，对长笔记不公平。 注意：一味追求短期消费指标是不对的。举个例子，如果推荐算法只看用户短期兴趣，推很多用户最近感兴趣的内容，这些消费指标上涨，这样的坏处是会竭泽而渔，用户会很快失去兴趣，不再回来；反过来，如果把多样性做好，尝试一些用户没看过的话题，那么点击率不会上涨，但是会有利于提高用户粘性，留住用户，让用户更活跃。

衡量推荐系统的好坏，最重要的指标叫北极星指标，即最关键的指标，是衡量推荐系统好坏的根本标准。北极星指标：

• 用户规模：DAU， MAU
• 消费：人均使用推荐的时长，人均阅读笔记的数量
• 发布：发布渗透率、人均发布量

实验流程：

• 离线实验
  • 收集历史数据，在历史数据上做训练、测试。算法没有部署到产品中，没有跟用户交互。
  • 结果有参考价值，但没有线上实验可靠，也无法得到线上指标。
• 小流量AB测试
  • 算法部署到实际产品中，用户实际跟算法做交互。
  • 可以得到线上指标，如北极星指标。
• 全流量上线

概要02 推荐系统的链路

--几亿物品--> 召回 --几千物品--> 粗排 --几百物品--> 精排 --几百物品--> 重排 --几十物品-->

• 召回
  • 当用户刷新小红书时，系统会同时调用几十条召回通道，每条召回通道取几十到几百笔记，一共取几千篇笔记
• 粗排
  • 用规模比较小的机器学习模型给几千篇笔记逐一打分，按照分数做排序和截断，保留分数最高的几百篇笔记
• 精排
  • 这里要用大规模的神经网络为几百篇笔记逐一打分，精排的分数反映出用户对笔记的兴趣
  • 精排之后，可以做截断，也可以不做截断。小红书的精排不做截断，几百篇笔记都带着精排分数进入重排
• 重排
  • 重排是最后一步，根据精排分数和多样性分数做随机抽样，得到几十篇笔记
  • 然后把相似内容打散，并且插入广告和运营内容
  • 重拍的规则非常复杂，有好几千行代码

粗排、精排的NN输入是用户特征，物品特征，和统计特征，NN输出点预估的击率，点赞率，收藏率，转发率。融合（加权和）预估值得到最终的排序分数。这个值会决定笔记是否会被展示给用户，靠前或靠后。重排最重要的是做多样性抽样，比如MMR、DPP，从几百篇中选出几十篇。抽样的时候有两个依据，一个是精排分数的大小，一个是多样性。做完抽样后，用规则打散相似笔记，我们不能把内容过于相似的笔记排在相邻的位置上。重排的另一个目的是插入广告、运营推广内容，根据生态要求调整排序，比如不能连着出美女图片。召回和粗排是最大的漏斗，它们让候选笔记的数量从几亿变成几千然后变成几百。当候选笔记之后几百才能用大规模NN做精排，用DPP做抽样。

概要03 推荐系统的AB测试

算法工程师的日常工作就是改进算法的策略，目标是提高推荐系统的业务指标。所有对模型的粗略的改进都需要进行线上的AB测试，用实验数据来验证试验策略是否有效。举个例子解释AB测试的目的是什么：

• 召回团队实现了一种GNN召回通道，离线实验结果正向。但是离线实验的指标有提升未必意味着线上实验也会有收益。
• 做完离线实验，下一步是做线上的小流量AB测试，考察新的召回通道对线上指标的影响，比如DAU，留存，交互等。
• 除了上述目的，模型中的一些参数，比如GNN的深度取值（1，2，3），需要用AB测试选取最优参数。可以同时开三组AB测试，哪组效果好用哪个。

做AB测试需要对用户做随机分桶，比方说：

• 分$b=10$个桶，每个桶中有10%的用户。如果用户的数量足够大，那么每个桶DAU，留存，点击率这些指标都是相等的。
• 首先用哈希函数把用户ID映射成某个区间内的整数，然后把这些整数随机分成$b$个桶。
• 以GNN为例，一号桶实验组#1，以此类推，四号桶为对照组
• 计算每个桶的业务指标，比如DAU，人均使用推荐的时长，点击率等。
• 如果某个实验组指标显著优于对照组，则说明对应的策略有效，值得推全，即把流量扩大到100%。

接下来讲分层实验，用业界实际上就是这么做的。分层实验的目标就是解决流量不够用的问题。举个例子解释，比方说小红书有很多个部门，每个部门有好几个团队，负责推荐系统（召回，粗排，精排，重排），用户界面，广告，所有团队同时需要做实验，线上需要做几十个甚至上百个实验。如果把用户随机分成10组，1组作对照，9组作实验，那么只能同时做9组实验，根本无法满足产品迭代的需求。解决方案就是分层实验：

• 把实验分成很多层，比如召回，粗排，精排，重排，用户界面，广告，…
• 同层是实验之间需要互斥：比如GNN实验占了召回层的4个桶，其他召回实验只能用剩余的6个桶。同层互斥的目的是避免一个用户同时被两个召回实验影响。如果两个实验相互干扰，实验结果会变的不可控。
• 不同层之间流量正交：每一层都独立随机对用户做分桶。每一层都可以独立用100%的用户做实验。召回和粗排的用户是独立随机划分的，召回的2号桶和粗排的2号桶交集很小。
• 分层实验参考文献 Tang et al. Overlapping experiment infrastructure: more, better, faster experimentation. In KDD, 2020. PDF

举个例子，召回层和精排层各自独立随机把用户分成10个桶：

• 召回层把用户分成10个桶：$u_1, u_2, …, u_{10}$
• 精排层把用户分成10个桶：$v_1, v_2, …, v_{10}$
• 设系统一共有$n$个用户，那么$\lvert u_i \rvert=\lvert v_j \rvert=n/10$
• 召回桶$u_i$和召回桶$u_j$的交集为$u_i \cap u_j=\varnothing$，即同层互斥，两个召回实验不会同时作用到同一用户上。
• 召回桶$u_i$和精排桶$v_j$的交集的大小为$\lvert u_i \cap v_j \rvert =n/100$。一个用户不能同时被两个召回实验影响，但可以同时受一个召回实验和一个精排实验影响。一个召回实验和一个精排实验各自作用在$n/10$个用户上，那么有$n/100$的用户同时被召回实验和精排实验影响，即不同层正交。

互斥 vs 正交：

• 如果所有实验都正交，则可以同时做无数组实验。
• 同类的策略（例如精排模型的两种结构）天然互斥，对于一个用户，只能用其中一种。
• 同类的策略（例如添加两条召回通道）效果会相互增强（1+1>2）。互斥可以避免同类策略相互干扰。
• 不同类型的策略（例如添加召回通道、优化粗排模型）通常不会相互干扰（1+1=2），可以作为正交的两层。

前面讲了AB测试的原理和分层实验，接下来介绍holdout机制：

• 每个实验（召回，粗排，精排，重排）独立汇报对业务指标的提升。一个实验通常由一两个算法工程师负责，如果有提升，那么就是算法工程师自己的业绩。
• 公司需要考察一个部门在一段时间内对业务指标总体的提升，比如推荐部门在两个月内的成果。不能简单地把所有推荐指标的收益都加起来作为部门整体业绩，这样相加是不可信的。实验叠加到一起通常会有折损。
• 所有需要holdout机制，取10%的用户作为holdout桶，推荐系统使用剩余90%的用户做实验，两者互斥。
• 只要算一下两者（10%holdout桶和90%实验桶）的diff（需要归一化）即可作为整个部门的业务指标收益。
• 在每个考核周期结束之后，会清除holdout桶，让退全实验从90%的用户扩大到100%的用户。
• 然后随机重新划分用户，得到holdout桶和实验桶，开始下一轮考核周期。
• 由于划分是随机均匀的，新的holdout桶与实验桶各种业务指标diff接近0，可以开始公平实验对比。
• 在新的考核周期开始之后，会有召回，粗排，精排，重排的实验上线和推全，diff会之间扩大。

这节课随后一部分内容是实验推全&反转实验：

推荐系统中所有实验都是从小流量开始的，如果业务指标显著正向，则可以推全实验。举个例子，我们做一个重排策略实验，取一个桶作为实验组，一个桶作为对照组，实验一共影响了20%的用户，如果观测到显著正向的业务指标收益，则可以推全这个策略，把重排层实验过点，这样就能把两个桶空出来给其他实验用。推全的时候新开一层，新策略会影响全部90%的用户。在小流量阶段，新策略作用到10%用户上，会微弱地提升实验桶和holdout桶的diff。推全之后，新策略作用到90%用户上，diff会扩大9倍。比方说AB测试发现新策略会提升点击率9个万分点，小流量实验之作用到10%的用户上，所以只能把和holdout桶的diff提升1个万分点，推全之后，理论上可以把diff提升到9个万分点，跟AB测试得到的数据一致。

接下来讲反转实验。上线一个有效的策略之后，需要观测很多业务指标：

有的指标（点击，交互类如点赞、完播）会立刻收到新策略的影响，而有的指标（留存）有滞后性，需要长期观测。比如点击率、点赞率等指标会立刻收到新策略的影响，实验上线一天或者实验上线十天，观测到的指标差距不会太大。用户使用的时长，人均阅读量这些指标有些滞后，需要多观察几天指标才会稳定。用户留存指标滞后非常严重，有可能短期内观测不到显著变化，但在之后几个月会持续改善。指标滞后的原因不难理解，新策略改善用户体验，过一段时间才能倍用户感受到，感受到之后，用户对产品的粘性越来越高。也就是说，实验观测的越久越好，可以让观测到的指标跟准确。

但算法工程师希望在观测到显著收益之后，一两周就推全实验。这样有很多好处，可以腾出桶来给其他实验使用，活需要机遇新策略做后续实验开发。也就是说尽快推全有好处，实验保留很久很也有好处，这就是一对矛盾。实践中常用反转实验解决上述矛盾，既可以尽快推全，也可以长期观测实验指标。具体做法是在推全的新层开一个旧策略的桶，这样就可以长期观测实验指标。

我画一下反转实验的示意图，这是为推全新策略开的一层，新层与召回、粗排、精排、重拍全部正交，可以在这个新层里开一个很小的反转桶，桶里的用户都用旧策略。可以把反转桶保留很久，长期观察新策略与旧策略的diff。一个考核周期结束之后，会清除掉holdout桶，但这不会影响反转桶。清除holdout会把推全的新策略作用到holdout用户上，不会影响反转桶。当反转实验完成时，关闭反转实验，新策略会作用到反转桶的用户上，也就是实验真正推全，对所有用户都生效.

总结：

• 分层实验是工业界通用的做法，把容易相互增强或抵消的实验放在同一层。同层互斥（不允许两个实验同时影响一位用户），不同层正交（不同实验可以有重叠的用户）。
• Holdout也是工业界通用的机制，保留10%用户，完全不受实验影响，可以考察整个部门在两个月内对业务指标的总的贡献。
• 实验推全，意思是流量扩到到90%用户，每新建一个策略都会新建一个推全层，覆盖90%用户，与其他层正交。
• 反转实验，是为了尽早推全新策略的同时可以长期观察各种指标。具体做法是在新的推全层上，保留一个小反转桶，使用旧策略，可以把反转桶保留很久，长期观测新旧策略的diff。

召回

召回01 基于物品的协同过滤（ItemCF）

用一个通俗的例子解释ItemCF的原理：比方说我喜欢看《笑傲江湖》，《笑傲江湖》与《鹿鼎记》相似，而且我没有看过《鹿鼎记》，那么系统会给我推荐《鹿鼎记》。推荐的理由是两个物品很相似。系统通过历史记录可以知道我喜欢看《笑傲江湖》，而求没看到过《鹿鼎记》，但是推荐系统如何知道《笑傲江湖》与《鹿鼎记》相似呢？有很多种办法可以做到，比如用知识图谱，两本书的作者相同，所以两本书相似；还可以基于全体用户的行为判断物品的相似性，比如看过《笑傲江湖》的用户也看过《鹿鼎记》，给《笑傲江湖》写好评的用户也给《鹿鼎记》写好评，我们可以从用户的行为中挖掘出物品的相似性，用物品之间的相似性做推荐。

下面讲解ItemCF的实现：每个用户都交互过若干个物品，比如点击、点赞、收藏、转发过的物品。可以量化用户对物品的兴趣，比如点击、点赞、收藏、转发这四种行为个算一分。在这个例子中，用户对四个物品的兴趣分数$like(user, item_j)$分别是2，1，4，3。对于用户没有交互过的候选物品，我们要决定是否把这个物品推荐给用户。假设我们知道物品两两之间的相似度，比如他们的相似度$sim(item_j, item)$分别是0.1,0.4,0.2,0.6,后面会详细讲解相似度是如何计算的，用下面的公式来预估用户对候选物品的兴趣：

在这个例子中，从用户到候选物品有4个路径，所以要计算四个分数把他们相加，计算$2 \times 0.1 + 1 \times 0.4 + 4 \times 0.2 + 3 \times 0.6 = 3.2$，表示用户对候选物品的兴趣。举个例子，有2000个候选物品，我们逐一计算用户对候选物品的兴趣分数，然后返回其中分数最高的100个物品。

我们来看看具体如何计算两个物品的相似度：

• 两个物品的受众重合度越高，两个物品越相似。我们可以从数据中挖掘出物品的相似度。
• 相似例子：喜欢《射雕英雄传》和《神雕侠侣》的读者重合度很高，因此可以认为《射雕英雄传》和《神雕侠侣》相似。
• 不相似例子：下面是一些用户，这些边表示用户喜欢物品，红色和绿色这两个物品的受众没有重合，这意味着两个物品不相似。蓝色和绿色的物品被判定为相似，这是因为两个物品的受众重合度非常高。

计算物品相似度：

• 喜欢物品$i_1$的用户记作集合$W_1$，喜欢物品$i_2$的用户记作集合$W_2$。
• 集合$W_1$和$W_2$的交集记作$V = W_1 \cap W_2$, $V$包含同时喜欢$i_1$和$i_2$的用户。
• $i_1$和$i_2$两个物品的相似度：

分子是集合$V$的大小，即对两个物品都感兴趣的人数，$V$类似。这样计算出的相似度一定是一个介于0到1之间的数（因为$V$的数值一定比$W_1$和$W_2$小），数值越大表示两个物品月相似。注意，这个公式没有考虑喜欢的程度$like(user, item)$。用这个公式，只要是喜欢就看做1，不喜欢就看做0。

• 如果想要用到喜欢的程度，需要改一下这个公式。比如点击、点赞、收藏、转发各自算1分，用户对物品的喜欢程度最多是4分。现在我们考虑用户对物品的喜欢程度：

分子把用户$v$对物品$i_1$和$i_2$的兴趣分数相乘取连加，连加是关于用户$v$取的，用户$v$同时喜欢两个物品。如果兴趣分数的取值是0或者1，那么分子就是同时喜欢两个物品的人数，也就是集合$V$的大小。公式的分母是两个根号的乘积，第一项是用户对物品$i_1$的兴趣分数的平方关于所有用户求连加然后开根号，第二项类似用户对物品$i_2$的兴趣分数的平方关于所有用户求连加然后开根号。这个公式计算出的数值介于0到1之间，表示两个物品的相似度。其实这个公式就是余弦相似度（cosine similarity），把一个物品表示为一个向量，向量每个元素对应一个用户，元素的指就是用户对物品的兴趣分数，两个向量的夹角的余弦就是这个公式。

小结：

• ItemCF的基本思想是根据物品的相似度做推荐，如果用户喜欢物品$i_1$，而且物品$i_1$与物品$i_2$相似，那么用户很可能喜欢物品$i_2$。
• 做推荐就需要预估用户对候选物品的兴趣有多强，给每个物品打一个分数，把分数高的物品推荐给用户。上面列出了预估兴趣分数的公式，需要用到用户的历史行为记录，对各个物品的兴趣，我们还需要知道物品$j$与候选物品的相似度，把两个数相乘，然后关于物品$j$取连加，作为用户对候选物品兴趣的预估。
• 这个公式需要知道物品两两之间的相似度，我们事先计算然后保存起来。上面列出了计算物品相似度的公式。

下面讲解ItemCF召回的完整流程：为了能在线上做到实时的推荐，系统必须要事先做离线计算，建立两个索引。

一个索引是“用户->物品”的索引：

• 记录每个用户最近点击、交互过的物品ID，比如最近交互过的两百个物品，每个物品还有相应的兴趣分数。
• 有了这个索引之后，给定任意用户ID，可以快速返回他近期感兴趣的物品列表。

另一个索引是“物品->物品”的索引：

• 我们首先要计算物品之间两两相似度，这个计算量会比较大。
• 对于每个物品，索引它最相似的k个物品，比如k=10或k=100。
• 有了这个索引之后，给定任意物品ID，可以快速返回与它最相似的k个物品，而且知道相似度分数。

有了索引之后，我们可以在线上给用户做实时推荐。比如：

1. 现在有个用户刷小红书，系统知道这个用户的ID，首先查看“用户->物品”索引，可以快速找到用户近期感兴趣的物品列表（last-n）。
2. 对于last-n集合中的每个物品，通过“物品->物品”的索引，找到top-k相似物品。因此，一用返回nk个物品。
3. 对于取回的相似物品（最多有nk个），用公式预估用物对物品的兴趣分数。
4. 按照分数从高到低对物品做排序，返回分数最高的100个物品，这一百个物品就是itemCF这个召回通道的输出，会跟其他召回通道的输出融合起来，然后做排序，最终展示给用户。

为什么要用索引呢？数据库有上亿个物品，如果挨个计算用户对所有物品的兴趣，计算量会爆，索引的意义在于避免枚举所有的物品。加入我们记录用户最近感兴趣的n=200个物品，取回每个物品最相似的k=10个物品，那么一共取回nk=2000个物品，用公式给这2000个物品打分（用户对物品的兴趣分数），返回分数最高的100个物品作为ItemCF通道的输出。这样的计算量是很小的，可以做到在线实时计算。总结一下，用索引的话，离线计算量大并需要更新两个索引，好处是线上计算量小，召回很快。这节课介绍 Swing 模型，它跟 ItemCF 非常类似，唯一

召回02 Swing模型

这节课介绍ItemCF的一个变体，叫做Swing，在工业界很常用。Swing跟ItemCF非常像，区别就是怎样定义物品的相似度。

此处省略recap on ItemCF的原理。下面讲ItemCF的不足之处，问题在于假如重合的用户是一个小圈子该怎么办。比方说这四个用户（四个用户都喜欢了item 1 和 item 2）都在同一个微信群里面，左边的item 1是这样的一篇笔记《某网站护肤品打折》，右边的物品item 2是笔记《字节裁员了》。这两篇笔记没有什么相似之处，他们的受众差别很大，但是两边笔记碰巧被分享到同一个微信群，群里有很多人同时点开这两篇笔记。这样就造城一个问题，两篇笔记的受众完全不同，但是很多用户同时交互过这两篇笔记，导致系统错误得判断两篇笔记的相似度很高。

想要解决这个问题，降低小圈子用户的权重，我们希望两个物品重合的用户广泛而且多样，而不是集中在一个小圈子里。一个小圈子的用户同时交互两个物品不能说明两个物品相似；反过来，如果大量不相关的用户同时交互两个物品，则说明两个物品有相同的受众。Swing的原理就是给用户设置权重，解决小圈子问题。

接下来讲Swing模型是怎么计算两个物品的相似度：

• 用户$u_1$喜欢的物品记作集合$J_1$
• 用户$u_2$喜欢的物品记作集合$J_2$
• 定义两个用户的重合度为$J_1$与$J_2$交集的大小，记作：

• 用户$u_1$和$u_2$的重合度越高，则他们越有可能是一个小圈子的人，要降低他们的权重。在计算物品相似度的时候，会把$overlap(u_1, u_2)$放到分母上。

Swing模型：

• 喜欢物品$i_1$的用户记作$W_1$，喜欢物品$i_2$的用户记作$W_2$
• 定义交集$V = W_1 \cap W_2$
• 两个物品的相似度

$\alpha$是一个人共设置的参数，需要调。如果两个人来自一个小圈子，重叠大，那么他们两个人对相似度的贡献比较小；反过来，如果overlap小，那他们对相似度的贡献比较大。用overlap可以降低小圈子对相似度的影响。

总结：

• Swing与ItemCF唯一的区别在于物品相似度
• ItemCF：两个物品重合的用户比例高，则判定两个物品相似
• Swing：额外考虑重合的用户是否来自于一个小圈子
  • 两个用户overlap大，则可能来一个小圈子，权重降低

召回03 基于用户的协同过滤（UserCF）

UserCF和ItemCF有很多相似之处，ItemCF是基于物品之间的相似度做推荐，UserCF是基于用户之间的相似度做推荐。

UserCF的原理：作为小红书的用户，我在小红书的点击点赞收藏转发可以体现出我的兴趣爱好，小红书上至少有几百个和我兴趣爱好非常相似的网友，虽然我不认识这些网友，但小红书可以从大数据中挖掘出来，小红书知道我们的兴趣爱好非常相似。今天其中某个跟我兴趣爱好非常相似的用户对某笔记点赞转发，于是小红书知道他喜欢这篇笔记，而我没看过这篇笔记，那么推荐系统就有可能给我推荐这篇笔记，推荐的理由就是跟我兴趣爱好的用户喜欢这篇笔记。

推荐系统如何找到跟我兴趣非常相似的网友呢？

• 方法一：点击、点赞、收藏、转发的笔记有很大的重合。每个用户都有一个列表，上面存储了交互过的笔记ID，对比两个用户的列表，就知道有多大的重合，重合越多说明两个人的兴趣越相似。
• 方法二：关注的作者有多大重合。每个用户都会关注一些作者，对比两个用户关注的作者列表，就知道有多少关注的作者是重合的。关注的作者重合越多说明两个人的兴趣越相似。

UserCF的实现：在用UserCF做推荐之前，需要先离线算好每两个用户之间的相似度，计算相似度的方法稍后再讲。在这个例子中，我们想要给左边的用户做推荐，右边是最相似的四个用户，用户之间的相似度$sim(user, user_j)=0.9, 0.7, 0.7, 0.4$。右边是候选物品，用户还没有看过这个候选物品，我们想要预估左边的用户对右边的候选物品兴趣有多大。历史数据反映了用户对候选物品的兴趣$like(user_j, item)=0, 1, 3, 0$，0表示用户没有看过该物品或者对物品不感兴趣。用这个公式来预估用户对候选物品的兴趣：

在这个例子中，从用户到候选物品有4个路径，$0.9 \times 0 + 0.7 \times 1 + 0.7 \times 3 + 0.4 \times 0 = 2.8$，表示左边用户对候选物品的兴趣。举个例子，有2000个候选物品，我们逐一计算用户对候选物品的兴趣分数，然后返回其中分数最高的100个物品。

计算用户相似度：这里的相似度指的是有用户有共同的兴趣点。先举个例子什么样两个用户不相似，这个例子中两个用户不相似，他们喜欢的物品没有重合。这个例子中两个用户被判定为相似，这是因为两个用户喜欢的物品重合度非常高，他们的兴趣点相似。两个用户的相似度是这样计算的：

• 用户$u_1$的喜欢的物品记作集合$J_1$，用户$u_2$的喜欢的物品记作集合$J_2$
• 集合$W_1$和$W_2$的交集记作$I = J_1 \cap J_2$, $I$包含两个用户共通喜欢的物品
• $u_1$和$u_2$两个用户的相似度：

这个公式有个不足之处，公式同等对待热门和冷门物品，这是不对的。拿书籍推荐举个例子，《哈利波特》是非常热门的物品，不论是大学教授还是中学生都喜欢《哈利波特》，既然所有人都喜欢看《哈利波特》，那么《哈利波特》对于计算用户相似度是没有价值的，越热门的物品越无法反映出用户独特的性质，对计算相似度久没有用；反过来，重合的物品越冷门，越能反映出用户的兴趣，如果两个用户都喜欢《Deep Learning》这本书，说明两个人很有可能是同行，如果两个人都喜欢更冷门些的书《Deep Learning for NLP and Speech Recognition》，说明两个人是小同行。为了更好得计算用户兴趣的相似度，我们需要降低热门物品的权重。前面计算用户相似度的公式可以等价改写成这种形式：

这里的分子还是集合$I$的大小，只不过换了种写法，写成了对1对连加，连加符号中的$l$是物品的序号，连加中的1是物品的权重，所有物品的权重都相同。刚才我们讨论了物品权重应该跟热门程度相关，越热门应该权重越低。我们把分子中的1换成第$l$物品的权重，$n_l$是喜欢物品$l$的用户数量，反映物品的热门程度。

小结：

• UserCF基本思想：
  • 如果用户1跟用户2相似，而且用户2喜欢某物品，那么用户1也很可能喜欢该物品
• 预估用户对候选物品的兴趣
• 计算两个用户的相似度
  • 每个用户表示为一个稀疏向量，每个元素对应一个物品
  • 相似度sim就是两个向量夹角的余弦

UserCF召回的完整流程 实现做离线计算需要先建立两个索引

• “用户->物品”的索引
  • 记录每个用户最近点击、交互过的物品ID
  • 给定任意用户ID，可以很快找到他近期感兴趣的物品列表及其兴趣分数
• “用户->用户”的索引
  • 这个跟ItemCF不同，ItemCF用的是“物品->物品”的索引，这里用的是“用户->用户”的索引，建立这个索引的方法几乎跟ItemCF相同
  • 对于每个用户，索引他最相似的k个用户，比如k=10 or 100，这个计算量会比较大
  • 给定任意用户ID，可以很快找到与他最相似的k个用户及其相似度
• 线上做召回
  • 给定用户ID，通过“用户->用户”的索引，找到top-k相似用户
  • 对于每个top-k相似用户， 通过“用户->物品”的索引，找到用户近期感兴趣的物品列别（last-n）
  • 对于召回的nk个相似物品，用公式预估用户对每个物品的兴趣分数
  • 返回分数最高的100个物品，作为召回结果

召回04 离散特征处理

前面几节课介绍了协同过滤的几种方法，后面几节课要介绍向量召回，在介绍向量召回之前，大家先熟悉一下离散特征的处理。这节课的重点是one-hot编码和embedding，有机器学习基础的同学可以跳过这节课。

离散特征在推荐系统中非常常见，比如性别（2），国籍（200+），英文单词（几万个），物品ID（小红书有几亿篇笔记，每篇笔记有一个ID），用户ID（小红书有几亿用户，每个用户有一个ID），这样的离散特征处理比较困难，因为数量实在太大了。推荐系统会把一个ID映射成一个向量。离散特征的处理分两步：

1. 建立字典：把类别映射成序号
2. 向量化：把序号映射成向量
   • one-hot编码：把序号映射成高维稀疏向量
   • embedding：把序号映射成低维稠密向量

此处省略one-hot编码的介绍，下面讲解one-hot编码的局限。例1：自然语言处理中，对单词做编码，英文有几万个单词，那么one-hot向量的维度是几万，这个维度是很大的，实践通常不会用这么高维的向量。例1：推荐系统中，需要对物品ID做编码，小红书有几亿篇笔记，那么one-hot向量的维度就是几亿，在实践中更难处理。在类别数量太大时，通常不用one-hot编码。对于性别这样的离散特征，类别数量很小，直接用one-hot向量;但是对于单词，ID这样的离散特征，类别数量巨大，用one-hot向量并不合适，更常见的做法是embedding，即每个类别映射成一个低维的稠密向量。

下面介绍embedding（嵌入），它是另一种把序号映射成向量的方法。我用两个例子讲解embedding：

例1: 国籍的embedding。字典里有中国、美国、印度、日本、德国等国家。字典把每个国家映射成一个序号比如1，2，3，…，200。Embedding把每个序号映射成一个向量，这些向量都是低维向量，比如向量大小都是(4,1)，一个向量就是对一个国家的表示，未知国籍就用全零向量表示。我们来分析一下参数的数量：

• 参数数量：向量维度 $\times$ 类别数量
  • 设embedding得到的向量都是4维的
  • 一共200个国籍
  • 参数数量 = $4 \times 200 = 800$
• 编程实现：TensorFlow、Pytorch提供embedding层
  • 在训练神经网络的时候，会自动做反向传播，学习embedding层的参数
  • Embedding层的参数是一个矩阵，矩阵大小是向量维度 $\times$ 类别数量
  • Embedding层的输入是一个序号，比如“美国”的序号是2
  • Embedding层的输出是一个向量，即参数矩阵的一列，比如“美国”对应参数矩阵的第2列

例1: 物品ID的embedding。假设物品的数据库里一共有10,000部电影，推荐系统的任务是给用户推荐电影。参数数量计算，设embedding向量的维度是16，参数数量 = $16 \times 10,000 = 160,000$。如果类别的数量不大，只有几百万，那么embedding层的实现是比较容易的，TensorFlow和Pytorch都可以处理得很好。但如果类别特别大，比如推荐系统中的物品数量有几十亿，那么emdedding层会特别大，一个神经网络绝大多数的参数都在embedding层，所以工业界深度学习系统都会对embedding层做很多优化，这是存储和计算效率的关键所在。

我画个示意图说明embedding得到的向量的物理意义。推荐系统具体怎么训练embedding层，下节课再讲。图中的每个点表示一个embedding，如果训练得好，从物品的embedding看一看出物品的特点。比如这些点都是动画片，它们的距离比较近，这些点都是间谍片，它们的距离也比较近，但是间谍片和动画片的距离比较远。

最后讲讲embedding和one-hot编码之间的关系。Embedding其实就是把一个one-hot向量乘到一个参数矩阵，即Embedding = 参数矩阵$\times$ One-Hot向量。比如说这是一个one-hot向量，第三个元素是1，其余都是0，这是embedding层的参数矩阵。把矩阵和one-hot向量相乘法，等于取出参数矩阵的第三列，把这个作为输出。从这个角度看，embedding就是矩阵向量乘法，跟全链接层非常像。

总结：离散特征处理方法，即one-hot编码以及embedding。

召回05 矩阵补充、最近邻查找

这节课和后面几节课详细讲解向量召回。矩阵补充（Matrix completion）是向量召回最简单的一种方法，不过现在已经不太常用这种方法了。我讲解矩阵补充是为了帮助大家理解下节课的双塔模型。

上节课介绍了embedding，它可以把用户ID、物品ID映射成向量，我画的这个模型就是基于embedding做推荐。模型的输入是一个用户ID和一个物品ID，模型的输出是一个实数，是用户对物品兴趣的预估值，这个数越大，表示用户对物品越感兴趣。下面我们看一下模型的结构，左边的结构只有一个embedding层，把一个用户ID映射到一个向量，记作向量a；右边类似，映射物品ID到向量b，两个embedding层不共享参数。对向量a和b做内积$\langle a,b\rangle$得到一个实数作为模型输出。这个模型就是矩阵补充模型，接下来我会解释为什么这个模型叫做矩阵补充。

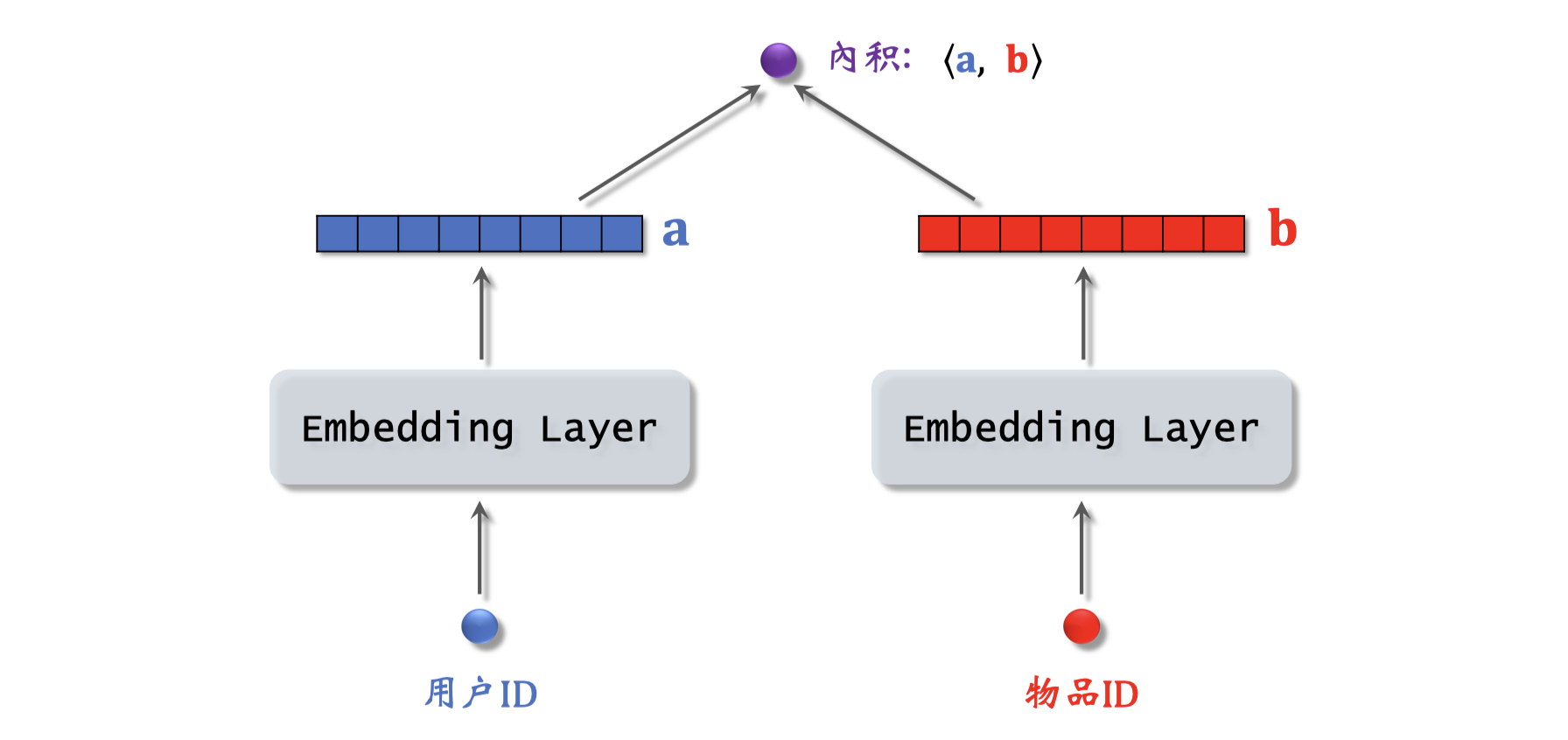
刚才定义了模型结构，接下来讲模型的训练。首先讲训练的基本思路：

• 用户embedding参数矩阵记作$A$。每个用户对应矩阵的一列，第$u$号用户对应矩阵的第$u$列，记作向量$a_u$
• 物品embedding参数矩阵记作$B$。每个物品对应矩阵的一列，第$i$号物品对应矩阵的第$i$列，记作向量$b_i$
• 内积$\langle a_u, b_i \rangle$是第$u$号用户对第$i$号物品兴趣的预估值
• 训练模型的目的是学习矩阵$A$和$B$，使得预估值拟合真是观测的兴趣分数

开始训练前，首先要准备一个数据集：（用户ID，物品ID，兴趣分数）的集合，记作$\Omega {(u,i,y)}$。训练时，求解优化问题，得到参数$A$和$B$：

我来解释一下为什么这个模型叫做矩阵补充。矩阵每一行对应一个用户，每一列对应一个物品，矩阵中的每一个元素表示用户对物品的兴趣分数。曝光过的笔记很少，因此矩阵非常sparse。有了训练号的模型，我们就可以预估没曝光物品的兴趣分数，把矩阵元素不全。之后就可以做推荐。但矩阵补充在实践中效果不好。

缺点1: 矩阵属性仅使用用户ID和物品ID的IDembedding，没利用物品、用户属性。在小红书，物品属性包括类目、关键词、地理位置、作者信息；用户属性包括性别、年龄、地理位置、感兴趣的类目。知道这些属性召回可以最得更精准。下节课的双塔模型可以看做矩阵补充的升级版。双塔模型不仅使用物品ID和用户ID，还使用各种物品属性和用户属性，双塔模型的实际表现非常好。

缺点2: 负样本的选取方式不对。这里的样本是用户-物品的二元组，记作$(u, i)$。训练向量召回模型需要正样本和负样本。正样本的选取是曝光之后，有点击、交互的物品（正确的做法）。负样本的选取是曝光之后，没有点击、交互的物品（错误的做法）。这是种想当然的做法，学术界的人可能以为这样没错，可惜这样在实践中不work。后面会有一节课讲解正负样本怎么选。

缺点3: 训练模型的方法不好。矩阵补充模型利用内积$\langle a_u, b_i \rangle$作为兴趣分数的预估，这样没错可以work，但是效果不如余弦相似度。工业界普遍使用余弦相似度。另外，矩阵补充用平方损失函数做回归任务，让预估的兴趣分数拟合真是的兴趣分数，不如使用交叉熵损失函数做分类任务。工业界通常做分类，判定一个样本是正还是负。

这节课剩下内容都是线上服务。在模型训练好之后，可以把模型用在推荐系统中的召回通道。做完模型训练之后，要把模型存储在正确的地方，便于召回：

1. 训练得到矩阵$A$和$B$，$A$的每一列对应一个用户，$B$的每一列对应一个物品
2. 把矩阵$A$的列存储到key-value表，key是用户ID，value是$A$的一列。这样给定一个用户ID，返回一个向量（用户embedding）
3. 矩阵$B$的存储和索引比较复杂，不能简单地用key-value存储。稍后解释原因以及解决办法。

在模型训练好，并且把embedding向量做存储之后，可以开始做线上服务：

1. 把用户ID记作key，查询key-value表，得到该用户向量$a$
2. 最近邻查找：查找用户最有可能感兴趣的k个物品，作为召回结果
   • 第i好物品的embedding$b_i$
   • 内积$\langle a, b_i \rangle$作为兴趣分数的预估
   • 返回内积最大的k个物品

这种最近林查找又个严重的问题，如果枚举所有物品，时间复杂度正比于物品数量，这种巨大的计算量是不可接受的，无法做到线上实时计算。这节课剩下内容就是加速最近邻查找，避免枚举。

有很多种算法加速最近邻查找，这些算法非常快，即使有几亿个物品，最多也只需要几万次内积（0.0001）。这些算法的结果未必是最优的，但不会比最优结果差多少。快速最近邻算法已经被集成到很多向量数据库系统中，比如Milvus、Faiss、HnswLib等等。作最近邻查找需要定义什么是最近邻，也就是衡量最近邻的标准：欧氏距离最小（L2距离），向量内积最大（内积相似度），目前推荐系统最常用的是向量夹角余弦最大（cosine相似度），即向量夹角最小的。有些系统不支持余弦相似度，但这很好解决，如果你把所有向量都做归一化，让它们的2范数全都等于1，那么内积就等于余弦相似度。

我用一个直观的例子来演示最近邻查找。这是个散点图，右边五角星标识一个用户的embedding记作向量$a$，我们想要召回这个用户可能感兴趣的物品，这就需要计算$a$与所有点的相似度，如果用枚举的话，计算量正比于物品数量。我们要避免暴力枚举，这里我介绍一种加速最近邻查找的算法。在做线上服务之前，数据做预处理，把数据划分成很多区域。至于如何划分，取决于衡量最近邻的标准。如果是cosine相似度，那么划分的结果是这样的扇形；如果用欧氏距离，那么结果就是多边形。划分之后，每个区域用一个向量表示，这些向量的长度都是1。划分区域之后，建立索引，把每个区域的向量作为key，把区域中所有点的列表作为value。假如有一亿个点，划分成一万个区域，索引上一共有一万个key值，给定一个向量，可以快速取回这个区域内所有的点。有了这样一个索引，就可以在线上快速作召回。在线上给一个用户作推荐，这个用户的embedding记作向量$a$，首先把$a$与索引中的向量作对比，计算相似度，因为如果一共几亿个物品索引向量只有几万而已，这一步的开销不大。之后，找到与$a$最相似的索引中的向量，通过索引，找到这个区域所有的点，即所有物品的embeeding。接下来，计算$a$与区域内所有点的相似度，如果一共几亿个物品被分到了几万个区域，平均每个区域只有几万个点，所以这一步只需要计算几万个相似度，计算量也不大。哪怕有几亿个物品，用这种近似算法做查找，只需要计算几万次相似度，比暴力枚举快一万倍。

总结：

• 矩阵补充
  • 物品ID，用户ID做embedding
  • 内积作为用户对物品的兴趣点预估
  • 让内积拟合真实观测到兴趣分数，学习模型的embedding层参数
  • 很多缺点，效果不好
• 线上召回
  • 用户向量作为query，查找是的内积最大化的物品
  • 暴力枚举速度太慢，实践中用近似最近邻查找

召回06 双塔模型–模型结构、训练方法

双塔模型可以看作矩阵补充的升级版，既用到用户ID和物品ID也用到用户和物品的特征。下面讲解模型结构。

我们先来看用户的特征，我们知道用户ID，还能从用户填写的资料和用户行为中获取很多特征，包括离散特征和连续特征。所有这些特征不能直接输入神经网络，而是要先做一些处理，比如用embedding层把用户ID映射成一个向量，跟上节课的做法相同。用户还有很多离散特征，比如所在城市，感兴趣的话题等，用embedding层把用户的离散特征映射成向量，对于每个离散特征用单独一个embedding层得到一个向量，对于性别这样类别数量很少的特征直接用one-hot编码就行可以不做embedding。用户还有很多连续特征，比如年龄、活跃程度、消费金额等。不同类型的连续特征需要不同的处理方法，最简单的事做归一化（均值0标准差1）；有些长尾分布的特征需要特殊处理，比如取log、做分桶。昨晚特征处理，得到很多特征向量，把这些向量都concatenate起来，输入神经网络，网络可以是简单的全链接网络或者更复杂的深度交叉网络。神经网络输出一个向量，向量就是对用户的表征，作召回要用到这个向量。

物品的特征也是用类似的方法处理，物品ID、物品离散特征、物品连续特征，最后神经网络输出物品的表征向量，用于召回。

这样的模型就叫双塔模型。左边的塔提取用户特征得到向量$a$，右边的塔提取物品特征$b$。跟矩阵补充模型相比，双塔模型使用了ID之外的多种特征。两个向量做内积就是模型最终的输出，预估用户对物品的兴趣。现在更常用余弦相似度，意思是两个向量夹角的余弦值，它等于向量的内积除以$a$的二范数再除以$b$的二范数，其实就相当于先对两个向量做归一化，再做内积，余弦相似度的大小介于-1和+1之间。

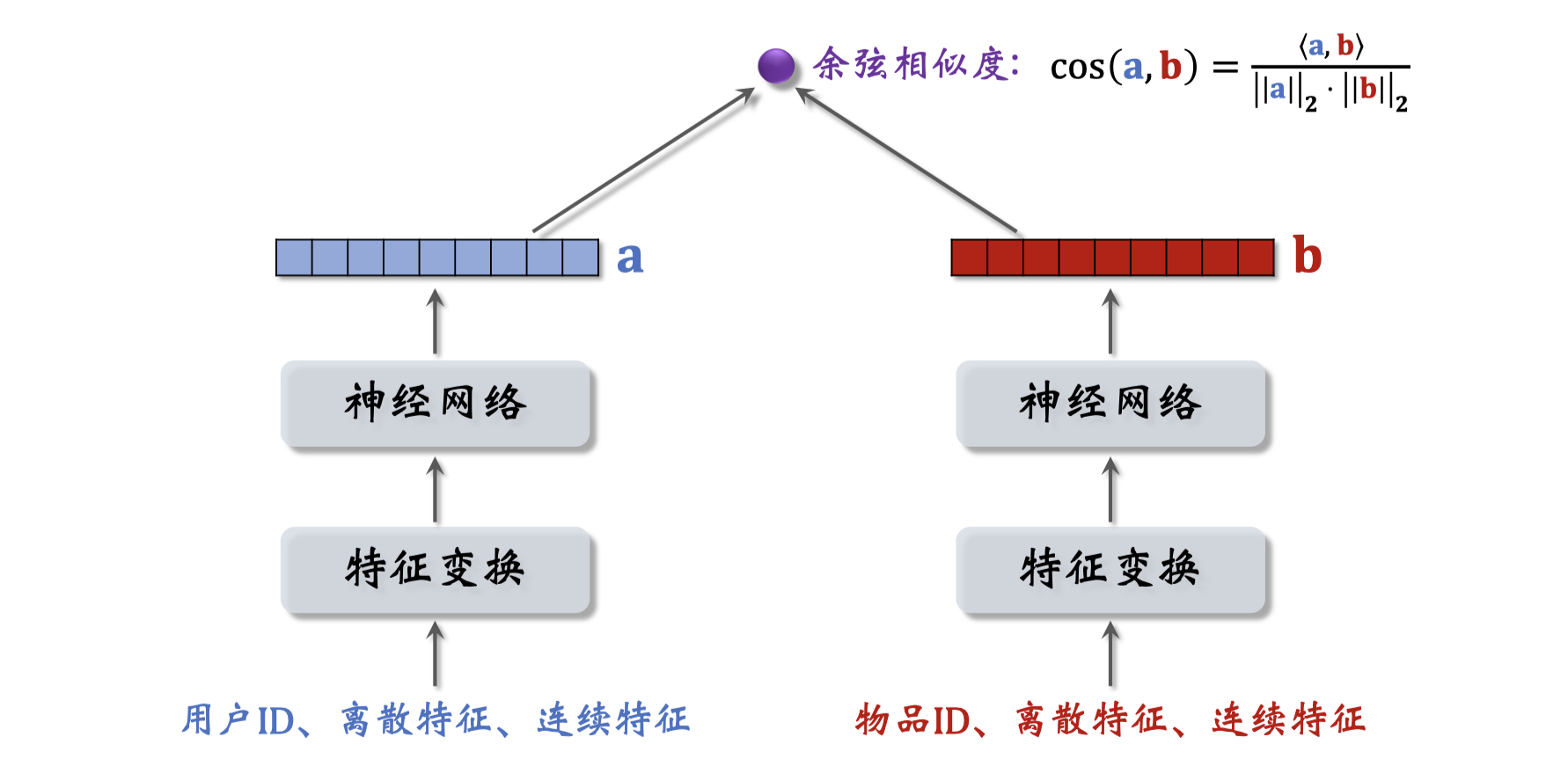
双塔模型的训练，有三种训练双塔模型的方式：

• Pointwise：独⽴看待每个正样本、负样本，做简单的⼆元分类
• Pairwise：每次取⼀个正样本、⼀个负样本组成一个二元组，损失函数用Triplot hinge loss或者Triplot logistic loss 参考文献 Jui-Ting Huang et al. Embedding-based Retrieval in Facebook Search. In KDD, 2020.
• Listwise：每次取⼀个正样本、多个负样本组成一个list，训练方式类似于多元分类， 参考文献 Xinyang Yi et al. Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations. In RecSys, 2019.

正负样本的选择：

• 正样本（感兴趣的物品）：用户点击的物品
• 负样本（0：负样本是用户不感兴趣的物品，负样本的选择没有那么显然，实践中负样本的选择是比较讲究的。有几种看起来比较合理的负样本：
  • 没有被召回的物品？
  • 召回但是被粗排、精排淘汰的？
  • 曝光但是未被点击的？

该用哪种呢？下节课再详细讲解。感兴趣的话可以自己阅读刚才提到的两篇文献，论文讲解了Facebook和Youtube如何选择正负样本，小红书基本是照做的，再加一些自己的小技巧，取得了很好的效果。

下面具体讲解训练双塔模型的方式。第一种Pointwise训练，也是最简单的训练方式：

• 把召回看做简单的⼆元分类任务。
• 对于正样本，⿎励$\cos(a,b)$接近+1。
• 对于负样本，⿎励$\cos(a,b)$接近−1。
• 控制正负样本数量为1:2或者1:3，我也不知道为什么，但是互联网大厂的人都这么做，这算是业内的经验。

第二种训练双塔模型的方式是Pairwise训练：

• 每一组输入是一个三元组，一个物品正样本，一个用户，一个物品负样本
• 基本想法：⿎励$\cos(a,b^{+})$⼤于$\cos(a,b^{-})$
• 如果$\cos(a,b^{+})$⼤于$\cos(a,b^{-}) + m$，则没有损失
• 否则，损失等于$\cos(a,b^{-}) + m - \cos(a,b^{+})$
• 这样就推导出了Triplet hinge loss

• 还有别的损失函数，比如Triplet logistic loss

这里$\sigma$是个大于0的超参数，控制损失函数的形状，$\sigma$需要手动设置。

第三种训练双塔模型的方式是Listwise训练：

• ⼀条数据包含：
  • ⼀个⽤户，特征向量记作$a$
  • ⼀个正样本，特征向量记作$b^+$
  • 多个负样本，特征向量记作$b_1^-,…, $b_n^-$
• ⿎励$\cos(a, b^+)$尽量⼤，$\cos(a, b_n^-)$尽量⼩
• Listwise训练具体做法：
  • 将$a$和$b^+$的余弦相似度，以及$a$和$b_n^-$的余弦相似度，(n+1)个值输入Softmax激活函数，输出值$s^+$, $s_1^-, s_n^-$在0到1之间，我们希望$s^+$越大越好最好是能接近1，$s_n^-$越小越好最好接近0
  • 样本标签$y^+ = 1, y_n^- = 0$，我们用$y$和$s$到交叉熵CrossEntropyLoss(y,s)做损失函数，训练时最小化交叉熵，即鼓励softmax输出接近标签$y$。其实交叉熵$\text{CrossEntropyLoss}(y, s) = - \log s^+$，最小化交叉熵就是最大化正样本的余弦相似度，最小化负样本的余弦相似度。

总结：

• ⽤户塔、物品塔各输出⼀个向量。
• 两个向量的余弦相似度作为兴趣的预估值。
• 三种训练⽅式：
  • Pointwise：每次⽤⼀个⽤户、⼀个物品（可正可负）。
  • Pairwise：每次⽤⼀个⽤户、⼀个正样本、⼀个负样本。
  • Listwise：每次⽤⼀个⽤户、⼀个正样本、多个负样本。

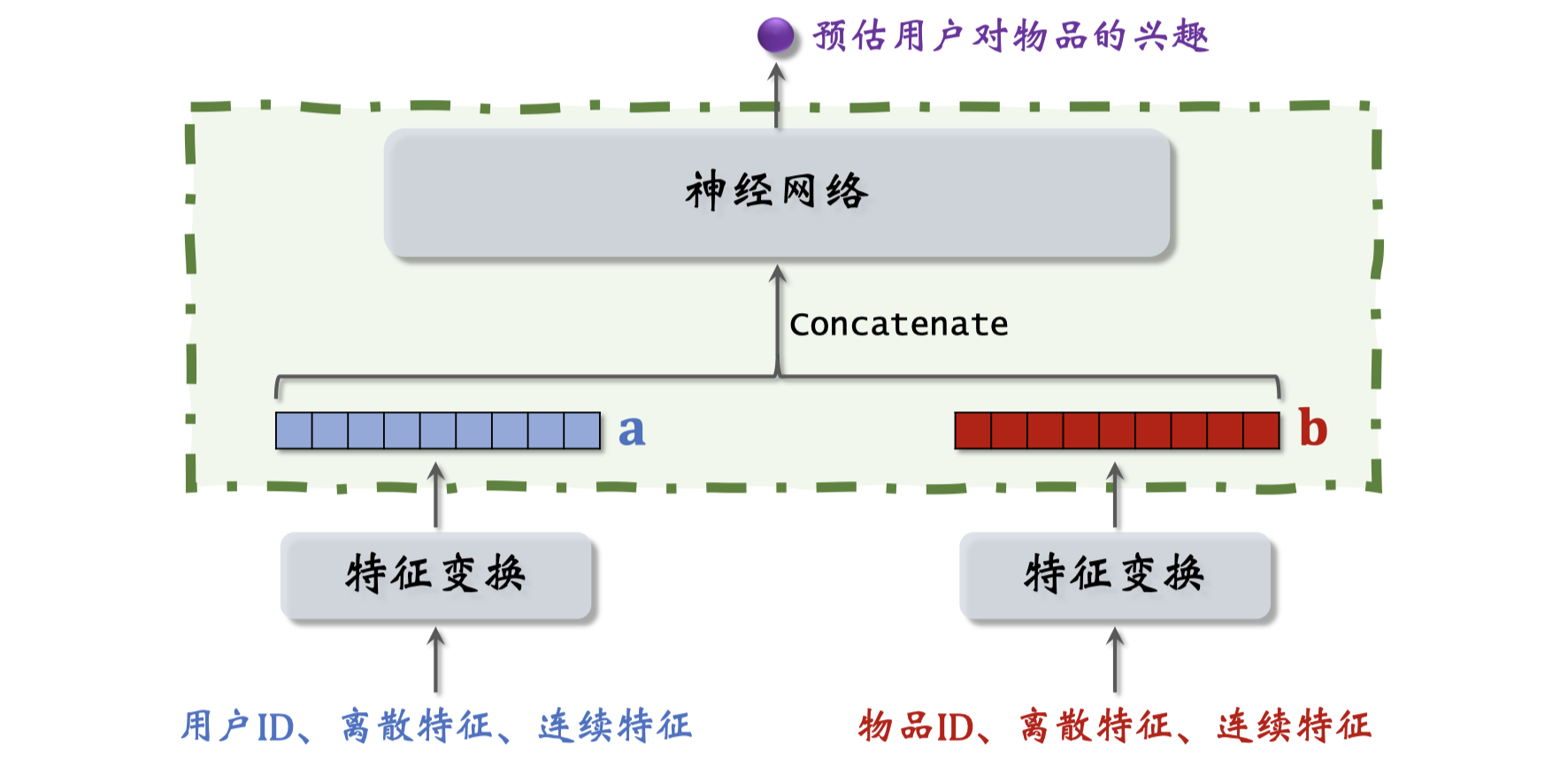
在结束这节课之前，我们讨论一种错误的召回模型的设计。大家一看到这种结构，应该知道这是粗排或者精排模型，而不是召回的模型。这种模型没办法应用在召回。下面这块结构和双塔模型是一样的，都是分别提取用户和物品的特征，但是上层结构就不一样了，这里直接把两个向量做concatenation，然后输入一个神经网络，神经网络可以有很多层。这种结构属于前期融合，在进入全链接层之前，就把特征向量拼起来了。这种前期融合的神经网络结构跟双塔模型有很大区别。双塔模型属于后期融合，两个塔在最终输出相似度的时候融合起来。图中这种前期融合的模型不适合召回，假如用到召回，就必须把所有物品的特征都挨个输入模型，预估用户对所有物品的兴趣。假设一共有一亿个物品，每给用户做一次召回，就要把这个模型跑一亿次，这种计算量显然不可行。这种模型通常用于排序，从几千个候选物品中选出几百个，计算量不会太大。以后大家只要一看到这种前期融合的模型，就知道这是排序模型，不是召回模型。召回模型只能用后期融合模型。

召回07 双塔模型–正负样本

选对正负样本，作用大过改进模型结构。正样本比较好选：

• 正样本：曝光⽽且有点击的⽤户—物品⼆元组（⽤户对物品感兴趣）。
• 问题：二八法则，少部分物品占据⼤部分点击，导致正样本⼤多是热门物品。拿过多的热门物品做正样本，会对冷门物品不公平。这样会让热门物品更热，冷门物品更冷。
• 解决⽅案：过采样冷门物品，或降采样热门物品。
  • 过采样（up-sampling）：⼀个样本出现多次。
  • 降采样（down-sampling）：⼀些样本被抛弃。

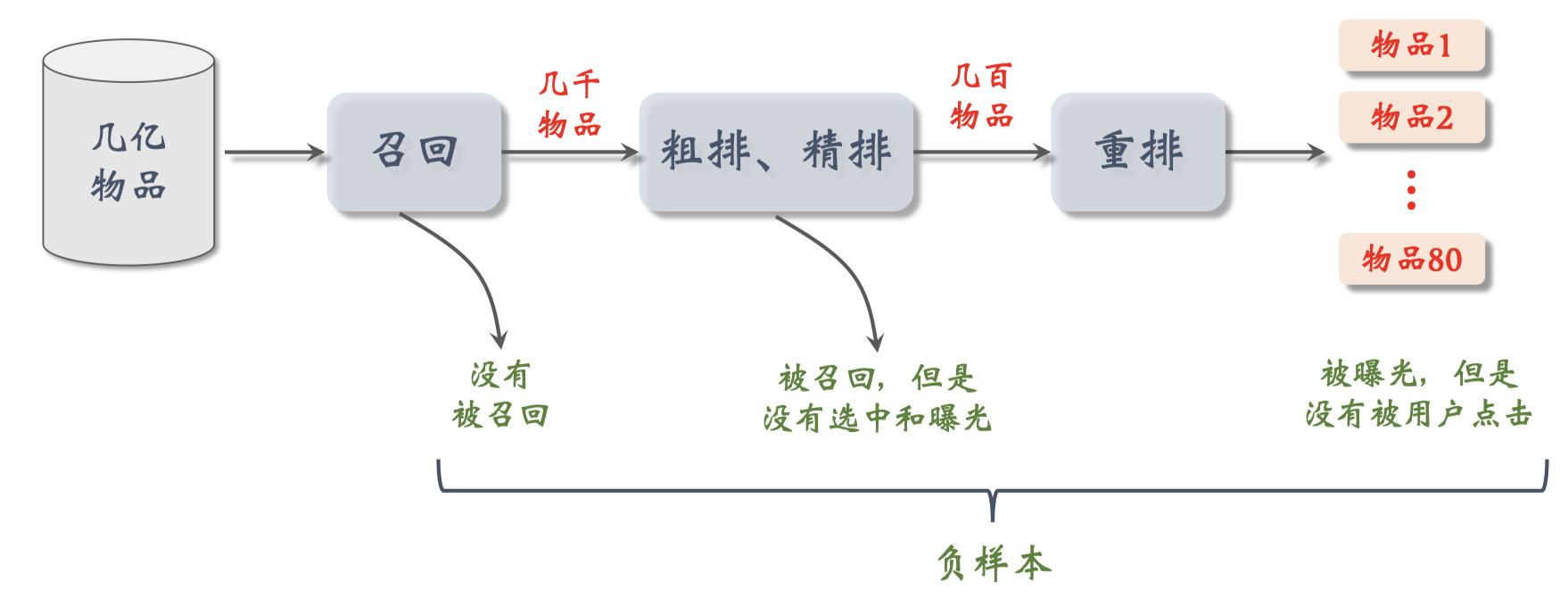
如何选择负样本? 接下来我们讨论这三种负样本。

简单负样本是未被召回的物品，⼤概率是⽤户不感兴趣的。因为被召回的物品只有几千，因此未被召回的物品 ≈ 全体物品。从全体物品中做抽样，作为负样本。问题是怎样抽样，均匀抽样or⾮均匀抽样？均匀抽样的坏处是对冷门物品不公平。正样本⼤多是热门物品。如果均匀抽样产⽣负样本，负样本⼤多是冷门物品。总拿热门物品做正样本，冷门物品做负样本，对冷门物品不公平。这样会让热门物品更热，冷门物品更冷。所以负样本抽样要随机非均匀，⽬的是打压热门物品。负样本抽样概率与热门程度（点击次数）正相关。热门物品成为负样本的概率大。物品的热门度可以用它的点击次数来衡量，可以这样做抽样$\text{抽样概率} \propto \text{点击次数}^{0.75}$，0.75是个经验值。

刚才介绍的简单负样本，是从全体物品内抽的。下面接受另一种简单负样本：Batch内负样本。⼀个batch内有$n$个正样本(user-clicked item pair)。⼀个⽤户可以和$n-1$个物品组成负样本。这个batch内⼀共有$n(n-1)$个负样本。都是简单负样本，因为对于第⼀个⽤户来说，第二个物品就相当于从全体物品中随机抽样的，用户大概率不会喜欢第二个物品。Batch内负样本存在一个问题。图中这些二元组都是通过点击行为选取的，所以一个物品出现在batch内的概率正比于它的点击次数（也就是它的热门程度）。这样就会有一个问题，物品成为负样本的概率本该是$\propto \text{点击次数}^{0.75}$，但在这⾥batch内负采样物品成为负样本的概率$\propto \text{点击次数}^1$。也就是说，热门物品成为负样本的概率过⼤。一个样品成为负样本的概率越大，模型对这个样品的打压就会越狠。对负样本应该打压，但这里打压太狠了，会造成偏差。这篇YouTube论文讲了如何修正偏差，我们在小红书照着做了，确实拿到了收益。

具体讲一下如何修正偏差，避免过分打压热门物品：

• 物品$i$被抽样到的概率：$p_i \propto \text{点击次数}$
• 预估⽤户对物品$i$的兴趣：$\cos(a, b_i)$
• 做训练的时候，调整为：$\cos(a, b_i) - \log{p_i}$
• 训练结束之后，在线上做召回时，还是用原本的余弦相似度$\cos(a, b_i)$

接下来介绍困难负样本，是被排序淘汰的物品。

• 物品被召回，但是被粗排淘汰（比较困难）。比方说召回5,000个物品进入粗排，粗排按照分数做截断，保留钱500个，那么被淘汰的4,500个物品都可以被视作负样本。为什么被粗排淘汰的物品较困难负样本呢？这戏物品被召回，说明它们跟用户兴趣多少有些关系；被粗排淘汰，说明用户对物品兴趣不够强，所以分成了负样本。对负样本做二元分类的话，困难负样本容易被分错，容易被判定为正样本。
• 精排分数靠后的物品（⾮常困难）。比方说精排给500个物品打分，排名在后300的样品都算是负样本。能够通过粗排进入精排，说明物品已经比较符合用户兴趣了，但未必是用户最感兴趣的，所以在精排中排名靠后的物品可以被视为负样本。

训练双塔模型是一个二元分类任务。全体物品（简单）分类准确率⾼。被粗排淘汰的物品（⽐较困难）容易分错。精排分数靠后的物品（⾮常困难）更容易分错。工业界比较常用的做法是把简单负样本和困难负样本混合起来作为训练数据。比如50%的负样本是全体物品（简单负样本），50%的负样本是没通过排序的物品（困难负样本）。

最后讨论一种常见的错误。很多人以为可以把曝光但是没有点击的物品作为负样本，其实这是错误的。如果你训练双塔模型的时候，用一些这样的负样本，效果肯定会变差，工业界的人已经踩过这个雷。为什么呢？因为一个物品能够通过精排模型的甄别曝光给用户，说明物品已经非常匹配用户的兴趣。每次给用户展示几十个物品，用户不可能每个物品都点击。没有点击不代表不感兴趣，可能只是用户对别的物品更感兴趣就点击了别的；或者用户感兴趣，可能碰巧没有点击。曝光没有点击的物品已经算是非常匹配的了，甚至可以拿来做召回的正样本，不应该作为召回的负样本。这是工业界的公示，是通过反复做实验得出的结论。

训练召回模型不能⽤这类负样本，训练排序模型会⽤这类负样本。我解释一下选择负样本的原理。召回的⽬标是快速找到⽤户可能感兴趣的物品，凡是用户可能感兴趣的全部取回来，然后再交给后面的排序模型逐一甄别。召回模型的任务是区分用户不感兴趣的物品和可能感兴趣的物品，而不是区分比较感兴趣的物品和非常感兴趣的物品。这就是选择负样本的基本思路。

• 可以把全体物品当做负样本（easy）：绝⼤多数是⽤户根本不感兴趣的。
• 被排序淘汰（hard）：⽤户可能感兴趣，但是不够感兴趣。
• 有曝光没点击（没⽤）：⽤户感兴趣，可能碰巧没有点击。（可以作为排序的负样本， 不能作为召回的负样本）

总结：

• 正样本： 曝光⽽且有点击。
• 简单负样本：全体物品，batch内负样本。
• 困难负样本：被召回，但是被排序淘汰。
• 错误：曝光、但是未点击的物品做召回的 负样本。

召回08 双塔模型–线上召回、模型更新

双塔模型的召回：

1. 离线存储：把物品向量存⼊向量数据库。
   • 完成训练之后，⽤物品塔计算每个物品的特征向量$b$。
   • 把⼏亿个物品向量$b$存⼊向量数据库（⽐如 Milvus、 Faiss、HnswLib ）。
   • 向量数据库建索引，以便加速最近邻查找。
2. 线上召回：查找⽤户最感兴趣的k个物品。
   • 给定⽤户ID和画像，线上⽤神经⽹络算⽤户向量$a$。
   • 最近邻查找：
     • 把向量$a$作为 query，调⽤向量数据库做最近邻查找。
     • 返回余弦相似度最⼤的k个物品，作为召回结果。

为什么事先存储物品向量$b$，线上现算⽤户向量$a$？

• 每做⼀次召回，⽤到⼀个⽤户向量$a$， ⼏亿物品向量$b$。（线上算物品向量的代价过⼤）
• ⽤户兴趣动态变化，⽽物品特征相对稳定。（可以离线存储⽤户向量，但不利于推荐效果）

模型更新：全量更新 vs 增量更新

1. 全量更新：今天凌晨，⽤昨天全天的数据训练模型。
   • 在昨天模型参数的基础上做训练，不是随机初始化。
   • ⽤昨天的数据，训练1 epoch，即每天数据只⽤⼀遍。
   • 发布新的 ⽤户塔神经⽹络 和 物品向量，供线上召回使⽤。
   • 全量更新对数据流、系统的要求⽐较低。因为全量更新不需要实时的数据流，对生成数据的速度没有要求，延迟一两个小时也没有关系。对系统要求低是因为每天只需要对用户神经网络和物品向量发布一次就够了。
2. 增量更新：做 online learning更新模型参数，每隔几十分钟/几小时就发布新的模型参数。
   • ⽤户兴趣会随时发⽣变化。
   • 对数据流要求很高，要实时收集线上数据，并做流式处理，⽣成TFRecord⽂件。
   • 对模型做 online learning，增量更新ID Embedding的参数（不更新神经⽹络其他部分的参数，全链接层都是锁住的不做增量更新，只有全量更新的时候，才会更新全链接层的参数）。也就是说从早到晚，训练数据不断生成，不断做梯度下降，更新模型embedding层参数。为什么增量更新时只更新embedding层参数而全量更新不仅更新embedding还更新全链接层参数？这主要是出于工程实现的考量。道理一两句话也解释不清楚（哈哈哈什么鬼）。
   • 发布⽤户ID Embedding的目的，是为了供⽤户塔在线上计算⽤户向量。⽤户ID Embedding是哈希表的形式，给定用户ID可以查出ID embedding向量。最新的⽤户ID Embedding可以捕捉到用户最新的兴趣点，对推荐很有帮助。发布⽤户ID Embedding这个过程会有延迟，在小红书刚上线online learning的时候这个过程会有小时级的延迟，通过对系统做优化，延迟可以降低到几十分钟甚至更短。
   • 也就是说，用户在小红书上产生行为几十分钟之后，他的用户向量就会被更新。他再次刷新小红书的时候，双塔模型会考虑到他最新的兴趣。

在小红书，模型机要做全量更新，也要做增量更新。今天凌晨做全量更新时，是基于昨日的全量模型，用昨天的数据，做全量更新，而不是用今天增量训练出来的模型。在完成这次全量训练之后，下面增量训练出来的模型就可以扔掉了。然后再基于今天凌晨全量训练出来的模型做分钟级别的增量跟新。从今天凌晨到明天凌晨，不停做online learning，每隔几十分钟发布一次模型。

问题：能否只做增量更新，不做全量更新？实践证明只做增量更新效果不好。

• ⼩时级数据有偏，它的统计值跟全天的数据差别很大（不同时间段用户行为不一样）；分钟级数据偏差更⼤，和全天统计值差别巨大。
• 全量更新：random shuffle ⼀天的数据，这样做就是为了消除偏差，做 1 epoch 训练。
• 增量更新：按照数据从早到晚的顺序，做 1 epoch 训练。
• 随机打乱数据做训练优于按顺序排列数据做训练，因此全量训练优于增量训练。

总结：双塔模型，线上召回，模型更新。具体内容略。

召回09 双塔模型+自监督学习

这节课介绍一种改进双塔模型的方法叫自监督学习，用在双塔模型上会提升业务指标。这种方法由谷歌在2021年提出，工业界（包括小红书）普遍验证有效。自监督学习的目的是为了把物品塔训练得更好。为什么要做自监督学习呢？在实际的推荐系统中，数据上的问题会影响模型的表现。

• 推荐系统的头部效应严重：少部分物品占据⼤部分点击，⼤部分物品的点击次数不⾼。
• 训练双塔模型时，用点击数据作为正样本，模型学习物品的表征，靠的就是点击行为。如果一个物品给几千个用户曝光被几百个用户点击。因此⾼点击物品的表征学得好，长尾物品的表征学得不好。这是因为长尾物品曝光和点击次数太少，训练样本数量不够。
• 一种比较好的解决方法：⾃监督学习，对物品做data augmentation，更好地学习长尾物品的向量表征。
• 参考文献：Tiansheng Yao et al. Self-supervised Learning for Large-scale Item Recommendations. In CIKM, 2021.

复习：双塔模型的训练。略。

损失函数：listwise训练双塔模型时，向量$p_i: p_{i,1}, p_{i,2}, …, p_{i,i}, …, p_{i,n}$，向量$y_i: 0, 0, …, 1, …, 0$，损失函数为：

前面正负样本课程讲过batch内负样本会过度打压热门物品，造成偏差。如果用batch内负样本就需要纠偏。这里再回顾一下：

• 物品$j$被抽到的概率$p_j \propto \text{点击次数}$，反映物品的热门程度
• 双塔模型用余弦相似度$\cos(a_i, b_j)$来预估用户$i$对物品$j$的兴趣程度
• 做训练时，要把$\cos(a_i, b_j)$替换成$\cos(a_i, b_j) - \log p_j$，这样起到纠偏的作用，热门物品不至于被打压
• 训练结束之后，线上召回时，还是用原本的余弦相似度$\cos(a_i, b_j)$

训练双塔模型

• 从点击数据中随机抽取$n$个⽤户—物品⼆元组，组成一个batch
• 双塔模型的损失函数(i对应用户i)： \(L_{\text{main}}[i] = -\log \left( \frac{\exp{(\cos(a_i, b_i) - \log p_i)}}{\sum_{j=1}^{n} \exp(\cos(a_i, b_j) - log p_j)} \right)\)
• 做梯度下降，减⼩损失函数：$\frac{1}{n}\sum_{i=1}^n L_{\text{main}}[i]$

刚次回顾了双塔模型的listwise训练方式，同时训练用户塔和物品塔，接下来用自监督学习训练物品塔。下面是两个不同的物品记作$i$和$j $，对两个物品的特征做随机变换，得到特征$i^\prime$和$j^\prime$，对两个物品的特征做另一种随机变换，得到特征$i^{\prime\prime}$和$j^{\prime\prime}$。把这些变换过的特征输入物品塔，模型一共只有一个物品塔，物品塔输出向量$b_i^\prime$， $b_i^{\prime\prime}$，物品$i$的这两个向量表征应该有有高的相似度。物品塔对物品$j$输出向量$b_j^\prime$和$bi_j^{\prime\prime}$，同样的道理，两个向量有很高的相似度。但是不同物品的向量表征应该离得尽量远，物品$i$和$j$的向量表征$b_i^\prime$和$b_j^{\prime\prime}$有较低的相似度。训练的时候，鼓励相同的物品的两个特征向量有尽量大的余弦相似度，而不同物品的特征向量有尽量小的余弦相似度。

自监督学习用到很多种特征变换，我挨个解释。

第一种是Random Mask：

• 随机选⼀些离散特征（⽐如类⽬），把它们遮住
• 举个例子：
  • 某物品的类⽬特征是$U$={数码, 摄影}，再对类目分别做embedding再取加和或者平均
  • Mask后的类⽬特征是$U^\prime$={default}，即默认缺失值，再对default做embedding，得到一个向量表征类目

第二种特征变换是Dropout，仅对多值离散特征⽣效。

• ⼀个物品可以有多个类⽬，那么类⽬是⼀个多值离散特征。
• Dropout：随机丢弃特征中50%的值。
• 举个例子：
• 某物品的类⽬特征是$U$={美妆，摄影}
• Dropout后的类⽬特征是$U^\prime$={美妆}

注意Random Mask和Dropout的区别，Mask是把整个类目特征都丢掉，而Dropout只丢掉类目中的某些值。

第三种特征变换时互补特征（complementary）。举个例子：

• 假设物品⼀共有4种特征：ID，类⽬，关键词，城市。正常的做法是把这四种特征分别作embedding，然后拼起来输入物品塔，最终得到物品的向量表征。
• 互补特征是指把特征随机分成两组：比如{ID，关键词} 和 {类⽬，城市}
• {ID，default，关键词，default} -物品塔-> 物品表征$b_{1,1}$
• {default，类⽬，default，城市} -物品塔-> 物品表征$b_{1,2}$
• 由于是对同一个物品的表征，这两个向量应该有比较高的相似度，训练的时候鼓励两个向量$b_{1,1}$和$b_{1,2}$相似度金量大

第四种特征变换是最复杂的，要随机遮住（mask）一组关联的特征。之所以用这种方法是因为特征之间有较强的关联，遮住一个特征并不会损失太多信息，模型可以从其他强关联特征中学到遮住的特征，最好是把关联特征一次全都遮住。举个例子：

• 物品的受众性别：$U$={男,⼥,中性}
• 物品的类目：$V$={美妆,数码,⾜球,摄影,科技,⋯}
• $u$=⼥和$v$=美妆同时出现的概率$p(u,v)$大
• $u$=男和$v$=美妆同时出现的概率$p(u,v)$小
• 因此，假如我们知道类目是美妆，那么受众性别大概率是女性

具体方法：

• 设$p(u)$为$U$特征取值为$u$的概率, 设$p(v)$为$V$特征取值为$v$的概率，$p(u,v)$是$u,v$同时发生的概率
• 离线计算特征两两之间的关联，用互信息（mutual information）衡量，两个特征关联越强，mutual infomation越大
• 计算特征$U$和$V$的mutual information：

这里不具体介绍互信息了，只需要知道两个特征关联强，$p(u,v)$就比较高。

• 设⼀共有$k$种特征。离线计算特征两两之间MI，得到$k \times k$的矩阵，表示特征之间的关联
• 每次随机选⼀个特征作为种⼦，找到种⼦最相关的$k/2$种特征
• Mask种⼦及其相关的$k/2$种特征，保留其余的$k/2$种特征

一组关联的特征的好处是实验效果好，⽐random mask、dropout、互补特征等⽅法效果更好。坏处是方法复杂，实现难度大，不容易维护，因为每添加一个新的特征，都需要重新算一遍所有特征的mutual information。在工业界通常会考虑投入产出比，为了指标再高一点，花更多的时间做开发，以后不好维护，可能不划算。

自监督学习模型训练损失函数：

• 从全体物品中均匀抽样，得到$m$个物品，作为⼀个batch
• 做两类特征变换，物品塔输出两组向量：$b_1^\prime, b_2^\prime, …, b_m^\prime$和$b_1^{\prime\prime}, b_2^{\prime\prime}, …, b_m^{\prime\prime}$
• 第 𝑖 个物品的损失函数：

• 一个batch中有$m$个物品，对$m$项损失函数取平均作为自监督学习的损失：$\frac{1}{m}\sum_{i=1}^m L_{\text{self}}[i]$

总结：

• 双塔模型学不好低曝光物品的向量表征
• 方法：⾃监督学习
• 实验效果非常好：低曝光物品、新物品的推荐变得更准。这些物品的点击率点赞率等指标都有显著提升，整个大盘的指标也有一定的改善

模型训练具体这样做：

• 每次对点击做随机抽样，得到$n$对⽤户—物品⼆元组，作为⼀个batch，这个batch用来训练双塔，包括用户塔和物品塔。根据点击做抽样，热门物品被抽到的概率高
• 每次还从全体物品中均匀抽样，得到$m$个物品，作为另⼀个batch。这样抽样的话，热门和冷门物品被抽到的概率是一样的。这个batch用来作自监督学习，只训练物品塔
• 做梯度下降，使得损失减⼩：

$L_{\text{main}}$是双塔模型的损失，$L_{\text{self}}$是自监督模型的损失，$\alpha$是个超参数，决定自监督学习起到的作用。

召回10 Deep Retrieval 召回

Deep Retrieval召回和之前讲的向量召回有相似之处，但区别也很明显。经典的双塔模型把⽤户、物品表⽰为向量，线上做最近邻查找。这节课介绍Deep Retrieval，它是字节发表的论文，据我所知Deep Retrieval已经在字节的一些业务线上落地了。Deep Retrieval的想法是把物品表征为路径（path），在线上查找⽤户最匹配的路径，从而召回一批物品。参考这篇字节论文：Weihao Gao et al. Learning A Retrievable Structure for Large-Scale Recommendations. In CIKM, 2021. Deep Retrieval的想法不是很新，它类似于阿⾥2018年发表的TDM，参考这篇阿里论文：Han Zhu et al。 Learning Tree-based Deep Model for Recommender Systems. In KDD, 2018。Deep Retrieval和TDM都用深度学习，但是它们都不做向量最近邻查找。TDM发表得更早，不过我觉得Deep Retrieval比TDM简单，所以我讲Deep Retrieval。

这节课内容分几部分：

1. 索引：
   • 路径 -> List<物品>
   • 物品 -> List<路径>
2. 预估模型：给定用户模型，神经⽹络可以预估⽤户对路径的兴趣
3. 线上召回：给定⽤户 -> 寻找他匹配的若干条路径 -> 召回每条路径对应的物品
4. Deep Retrieval的训练，同时学习两部分：
   • 学习神经⽹络参数
   • 学习物品表征（物品 -> 路径），把物品映射到路径

索引把物品和路径关联起来，Deep Retrieval把物品表示为路径。索引$\text{item} \rightarrow \text{List}<\text{path}>$: 一个物品可以对应多条路径。假设结构有3层，那就⽤3个节点表⽰⼀条路径：$\text{path} = [a,b,c]$。索引$\text{path} \rightarrow \text{List}<\text{item}>$: 一条路径会对应多个物品，线上作召回的时候需要甬道这个索引。给定一条路径，会取回很多物品作为召回的结果。

Deep Retrieval设计了一种神经网络，给定用户模型，神经⽹络可以预估⽤户对路径的兴趣分数。用这种神经网络，可以根据用户特征召回多条路径。下面讲怎样用神经网络预估用户对路径的兴趣：

• 假设结构有三层，⽤3个节点表⽰⼀条路径：$\text{path} = [a,b,c]$
• 给定⽤户特征$\mathbf{x}$，预估⽤户对节点$a$的兴趣$p_1(a \mid \mathbf{x})$
• 给定⽤户特征$\mathbf{x}$和节点$a$，预估⽤户对下一层的节点$b$的兴趣$ p_2(b \mid a; \mathbf{x})$
• 最后，给定⽤户特征$\mathbf{x}$和节点$a, b$，预估⽤户对再下一层节点$c$的兴趣$ p_3(c \mid a,b;\mathbf{x})$
• 神经网络模型预测用户对$\text{path} = [a,b,c]$兴趣：$p(a,b,c \mid \mathbf{x}) = p_1(a \mid \mathbf{x}) \times p_2(b \mid a; \mathbf{x}) \times p_3(c \mid a,b;\mathbf{x})$，后面的三项都是神经网络算出来的，乘积作为用户对路径的兴趣分数。

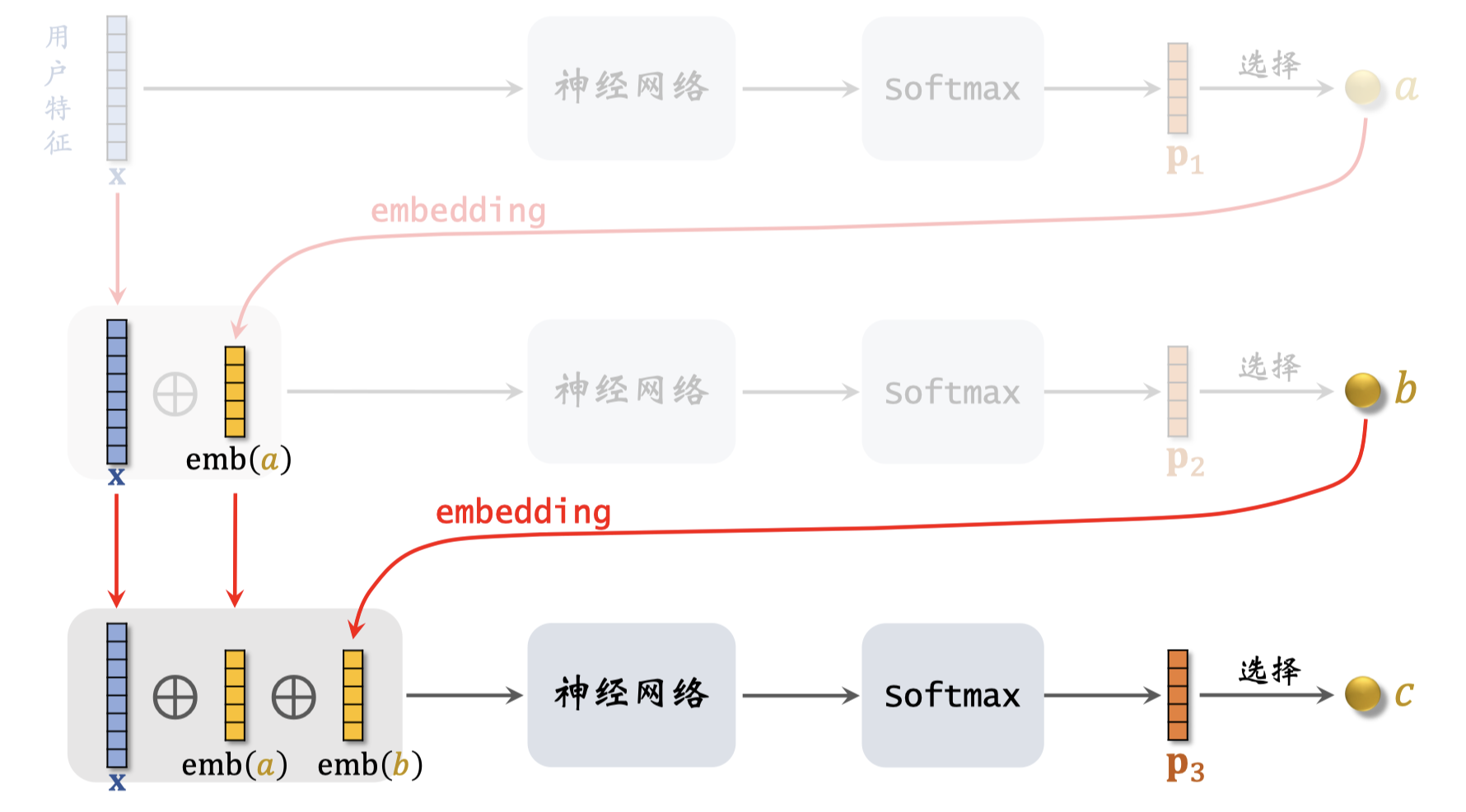
画图演示一下三层Deep Retrieval模型，每层$k$个节点。

• 第一层：模型的输入是用户特征$\mathbf{x}$，把它输入神经网络，神经网络最后是Softmax激活函数，把Softmax输出的向量记作$p_1$，如果结构的每一层有$k$个节点，那么$p_1$就是个$k$维向量。向量$p_1$对应L1层，$p_1$的$k$个元素是神经网络第L1层$k$个节点打的分数，分数越高节点也就越与可能被选中。根据向量$p_1$，我们从$k$个节点中选出一个节点记作$a$，论文里用beam search的方法选择节点，我后面会解释。
• 第二层：接下来，我们要把向量$\mathbf{x}$和节点$a$一起输入下一层神经网络，从结构的第二层中选出一个节点。向量$\mathbf{x}$不变，直接作为下一层的输入。对节点$a$作ebmedding，记作emb(a)，对$\mathbf{x}$和emb(a)作concatenation，然后输入另一个神经网络，这个神经网络的输出层也用Softmax激活函数，把Softmax输出的向量记作$p_2$，它也是个是个$k$维向量，对应结构中的第二层。向量$p_2$的$k$个元素是第L2层$k$个节点打的分数，根据分数从$k$个节点中选出选出一个节点记作$b$。
• 第三层：最后把向量$\mathbf{x}$和节点$a,b$一起输入下一层神经网络，即最后一层输入$\mathbf{x}$ + emb(a) + emb(b)，然后输入神经网络。在这个例子中一共有三层神经网络，它们不共享参数。下面这个神经网络的输出层也是Softmax，输出记作向量$p_3$，也是个$k$维向量，对应结构中的第三层。向量$p_3$的$k$个元素是第L3层$k$个节点打的分数，根据分数从$k$个节点中选出选出一个节点记作$c$。到此为止，我们已经从三层中各选出一个节点，组成了路径$[a, b, c]$。

下面介绍线上召回，给定用户特征召回一批物品。召回要从用户到路径再到物品：

• 召回第⼀步：给定⽤户特征，⽤beam search召回⼀批路径。
• 第二步：给定路径，利⽤索引$\text{path} \rightarrow \text{List}<\text{item}>$，召回⼀批物品。每条路径可以取回多个物品。
• 最后一步：对召回的物品做打分和排序，选出⼀个⼦集，作为Deep Retrieval召回通道的输出。

我们先讨论第一步，用Beam Search召回一批路径。假设Deep Retrieval的结构有3层，每层$k$个节点，那么一共有$k^3$条路径。⽤神经⽹络给所有$k^3$条路径打分，计算量太⼤。⽤beam search，可以减⼩计算量。需要设置超参数beam size。Beam size越大计算量越大，search的结果也会越好。先看下最简单的情况，即beam size = 1，每层都选分数最高的节点，组成路径。用户对路径$[a,b,c]$对兴趣分数：$p(a,b,c \mid \mathbf{x}) = p_1(a \mid \mathbf{x}) \times p_2(b \mid a; \mathbf{x}) \times p_3(c \mid a,b;\mathbf{x})$。最优的路径是分数最大的路径：$[a^\ast, b^\ast, c^\ast] = {\text{argmax}}_{a,b,c} p(a,b,c \mid \mathbf{x})$。beam size = 1 相当于贪心算法，选中的路径$[a,b,c]$未必是最优的路径，因为独立对$p_1, p_2, p_3$这三项求最大化未必会最大化这三项的乘积。如果把beam size设置大一些，结果会比贪心算法好，当然计算量也大。我演示一下beam size = 4的情况。第一步仍然是用神经网络给L1层的$k$个节点打分，选出分数最高的4个节点，所以从L1到L2有$4k$个路径。下一步要从这$4k$个路径中选出4条，我们要用神经网络计算用户对这4k$个路径的兴趣分数。

• 对于每个被选中的节点$a$, 即L1层中被选中的节点，我们要计算计算⽤户对路径$[a, b]$的兴趣：$p_1(a \mid \mathbf{x}) \times p_2(b \mid a; \mathbf{x})$
• 算出$4k$个分数，每个分数对应⼀条路径，选出分数top 4路径
• 以此类推第二层到第三层，注意排除掉没有没选中的路径，因此不是所有第一层到第二层的4个路径都会被选中

线上召回的第⼀步：给定⽤户特征，⽤神经⽹络做预估，⽤beam search 召回⼀批路径。Beam search是召回的第一步，也是最复杂的步骤。第⼆步：利⽤索引，召回⼀批物品，每条路径可以取回多个物品。路径和物品是怎么匹配上的，后面会讲。在线上做召回之前，线下已经把路径和物品匹配好了，已经有了从路径到物品的索引。做完前两步，已经取回了很多物品，很可能会超出这条召回通道的配额，所以要做个筛选，选出一个子集，作为Deep retrieval通道的输出。论文里面说要用到一个小的排序模型，给取回的物品打分，返回分数最高的一批物品。至于这个排序模型是什么，没有限制，你可以用双塔模型给召回的物品打分和排序。总之，deep retrieval做召回的话

线上召回： user -> path -> item

这节课剩下内容是离线作训练。训练时，要同时学习神经⽹络参数和物品表征。

• 神经⽹络$p_1(a,b,c \mid \mathbf{x})$预估⽤户对路径$[a,b,c]$的兴趣分数。做训练时，要学习这个神经网络的参数。
• ⼀个物品会被表征为多条路径${[a,b,c]}$，我们需要学习物品的表征，建⽴物品和路径的对应关系。学到物品的表征之后会建立两个索引：
  • $\text{item} \rightarrow \text{List}<\text{path}>$
  • $\text{path} \rightarrow \text{List}<\text{item}>$
• Deep retrieval做训练的时候只用到正样本(user，item)：click(user, item) = 1。正样本是物品和用户的二元组，只要用户点过物品就算是正样本。
• 假设我们把物品表征为$J$条路径：$[a_1,b_1,c_1], …, [a_J,b_J,c_J]$
• 用神经网络预估用户对路径$[a,b,c]$的兴趣$p(a,b,c \mid \mathbf{x})$
• 如果⽤户点击过物品，我们就认为⽤户对$J$条路径全都感兴趣
• 物品对这个物品感兴趣，应该让这$J$个加和变大，即$\text{argmax} \sum_{j=1}^J (a,b,c \mid \mathbf{x})$
• 损失函数：$\text{loss} = - \log \left( \sum_{j=1}^J (a,b,c \mid \mathbf{x}) \right)$。加和越大越好，对加和取负log作为损失函数。括号里的加和越大则损失越小。通过最小化这个损失函数来学习神经网络的参数。可以这样理解神经网络的训练：这个神经网络的作用是判断用户对路径有多感兴趣。如果用户点击过物品，我们就认为用户对物品的$J$条路径都感兴趣，应该让神经网络给这些路径打的分数更高。

刚才讲了如何学习训练神经网络的参数，训练过程中还要学习物品表征。

• ⽤户user对路径的$\text{path} = [a,b,c]$兴趣记作：$p(\text{path}\mid \text{user}) = p(a,b,c\mid x)$
• 物品item与路径path的相关性：$\text{score(item,path)} = \sum_{\text{user}} p(\text{path}\mid \text{user}) \times \text{click(user, item)}$。前面一项是神经网络预估的用户对路径的兴趣，后面一项点击是1，没点击是0。两项都有user，把两个分数相乘然后关于user取连加消除掉user。这个score越高说明这对物品和路径有越强的关联
• 几所物品和很多条路径的相关性分数，根据score(item,path)选出$J$条路径作为item的表征：$\Pi = \text{path}_1,…,\text{path}_J $
• 损失函数（选择与item高度相关的path）：$\text{loss}(\text{item}, \Pi) = -\log (\sum_{j=1}^{J}\text{score}(\text{item},\text{path}_j))$。对$J$条路径的分数取连加，这些路径与物品越相关，score的加和就越大。对连加取负log作为损失函数，选中的这条路径与物品越相关，损失函数就越小。假如我们最小化这个损失函数，那么就相当于根据分数score对路径作排序，取排序结果的top J。也就是说对于每个物品item，选择分数最高的$J$条路径，用这$J$条路径作为物品的表征。
• 但是简单取分数最高的$J$条路径不太好，存在问题。有可能发生这样的情况，非常多的物品集中在一条路径上。我们希望每条路径上的物品数量比较平衡，不希望少数路径上有超多物品。为了让路径上的物品尽量平衡，需要用正则项来约束path，论文上的正则项是路径上物品数量的四次方：$\text{reg}(\text{path}_j) = (\text{number of items on path}_j)^4$。如果一个路径上已经有了很多物品，这条路径就会受到惩罚，避免让它关联到更多的物品。

概括一下学习物品表征的算法，这是一种贪心算法，假设已经把物品表征成了$J$条路径，每次固定其中的$j-1$条路径$\text{path}_i(i \neq l)$，从未被选中的路径中，选出一条作为新的$\text{path}_l$关联到物品。

这样做选择，选中的路径有较高的分数，而且路径上的物品数量不会太多。

Deep Retrieval的训练分两块，一块是更新神经网络，另一块是更新物品的表征。交替做这两部分的训练，可以同时学到神经网络的物品表征。具体review内容略。

召回11 地理位置召回、作者召回、缓存召回

前面几节课讲解了集中最重要的召回通道，这节课简单介绍小红书用到其他召回通道。这几条召回通道很有用，但是重要性不高。

有一类是根据用户所在的地理位置做召回，GeoHash召回属于地理位置召回，之所以用这条召回通道，是因为用户可能对附近发生的事感兴趣，推荐系统应该出一些用户附近的内容。系统维护一个地理位置GeoHash索引。GeoHash是对经纬度编码成二进制哈希码，方便检索，这里你就当GeoHash是地图上一个长方形区域。索引是这样的，从GeoHash->优质笔记列表（按时间倒排）。也就是说以GeoHash作为索引，记录地图上一个长方形区域内的优质笔记，笔记列表按照时间顺序倒排。做召回的时候，给定用户的GeoHash，会取回这个区域内比较新的笔记。这条召回通道没有个性化，召回纯粹只看地理位置。就是因为没有个性化，我们才得用优质笔记，笔记本身质量好，即使没有个性化，用户也很有可能会喜欢看。反过来，既没有个性化，也不是优质笔记，那么召回的笔记大概率通不过粗排的精排。

GeoHash示意图，略。GeoHash召回很简单，如果用户允许小红书app获取用户定位，取回该地点最新发布的k篇优质笔记。至于这些笔记中有哪些符合用户的兴趣，会留待排序模型决定。

同城召回的原理是一样的，用户可能对同城发生的事感兴趣。索引：城市->优质笔记列表。做召回的时候，根据用户所在的城市和曾经生活过的城市。这条召回通道没有个性化。

前面讨论的地理位置召回，下面讨论作者召回。意思你如果你对一个作者感兴趣，系统就会给你推这个作者发布的新笔记。带社交属性的系统，都会有关注的作者这样一个召回通道。假如我在小红书上关注老梁，推荐系统就会时不时得给我推荐老梁发布的视频，尤其是在有新视频发布的时候，系统维护两个索引：用户->关注的作者，作者->发布的笔记。笔记的列表按照时间顺序倒排。线上做召回，给定用户ID->关注的所有作者->最新的笔记。

一种类似的召回通道是有交互的作者召回。原理是这样的，如果⽤户对某笔记感兴趣（点赞、收藏、转发）， 那么⽤户可能对该作者的其他笔记感兴趣。索引：⽤户->（最近一段时间内）有交互的作者。召回：⽤户->有交互的作者->最新的笔记。例子，我点赞了玉石雕刻视频，虽然我不收藏玉石，因此没有关注作者，但也应该给我推玉石雕刻视频，我很有可能看完。

另一条召回通道是相似作者召回。如果⽤户喜欢某作者，那么⽤户喜欢相似的作者。索引：作者->相似作者（k个作者）。召回：⽤户->感兴趣的作者(n)->相似作者(nk)->最新的笔记(nk篇笔记)。作者相似性的计算，类似于itemCF，如果两个作者的粉丝有很大的重合，那么就判定两个作者相似。

最后介绍缓存召回。想法：复⽤前n次推荐精排的结果。背景是这样的，小红书精排输出⼏百篇笔记，送⼊重排。重排做多样性随机抽样，比如用DPP选出⼏⼗篇曝光给用户。也就是说精排结果有⼀⼤半没有曝光，被浪费掉。这很可惜，好不容易走完召回，粗排，精排流程，只是碰巧随机抽样没被抽到，所以没有被曝光。应该想办法把这些笔记重新利用起来。小红书大致是这样做的，按照精排的分数做排序，精排前50，但是没有曝光的，缓存起来，作为⼀条召回通道。下次用户刷小红书的时候，把缓存里的笔记取出来，作为一路召回的结果。精排排到前50的，都是用户非常感兴趣的笔记，值得再次尝试。这种缓存召回有个问题，缓存大小固定，比如最多存一百篇笔记，每次就召回这一百篇笔记。由于缓存大小固定，那么就需要退场机制，确保缓存里最多有一百篇笔记。有很多条规则作为退场机制，比如⼀旦笔记成功曝光，就从缓存退场。如果超出缓存⼤⼩，就移除最先进⼊缓存的笔记。笔记最多被召回10次，达到10次就退场。每篇笔记最多保存3天，达到3天就退场。这些都是最简单粗暴的规则，在这些基础上，还能再细化规则。举个例子，假如想要扶持曝光比较低的笔记，那么可以根据笔记的曝光次数来设置规则，低曝光的笔记在缓存里存更长的时间。

总结这节课内容，三大类，一共六条召回通道：

• 地理位置召回：GeoHash，同城
• 作者召回：关注的作者，有交互的作者，相似的作者
• 缓存召回

召回12 曝光过滤 & Bloom Filter

曝光过滤通常是在召回阶段做，具体的方法就是用Bloom filter。曝光过滤是这样一个问题，在推荐系统中，如果⽤户看过某个物品，则不再把该物品曝光给这个⽤户。小红书和抖音都这样做曝光过滤，原因是实验表明重复曝光同一个物品会损害用户体验。但也不是虽有推荐系统都有曝光过滤，像YouTube这样的长视频就没有曝光过滤，看过的可以再次推荐。想要做曝光过滤，需要对于每个⽤户，记录已经曝光给他的物品。一个用户历史上看过对物品可能会非常多，好在不需要存储所有的历史记录，只需要存储最近一段时间的就行。以小红书推荐系统为例，只召回发布时间小于一个月的笔记，更老的笔记根本不会被召回，所以不用对年龄大于一个月的笔记做曝光过滤，只需要记录每个⽤户最近一个⽉的曝光历史，用它们做曝光过滤。在做完召回之后，对于每个召回的物品做曝光过滤，判断它是否已经给该⽤户曝光过，排除掉曾经曝光过的物品。⼀位⽤户看过n个物品，本次召回r个物品，如果靠暴⼒对⽐做曝光过滤，那么需要花费O(nr)的时间。在小红书，用户一个月的曝光量n的量级大约是几千，每次推荐召回量r的量级也是几千，暴力对比的计算量太大了，所以实践中不做暴力对比，是用Bloom filter。

Bloom filter是一种数据结构，发表于1970年，以它的发明者命名。推荐系统曝光过滤基本都是用bloom filter做的，它可以判断一个物品ID是否在已曝光的物品集合中。如果BF判断结果为no，那么该物品⼀定不在集合中。如果BF判断为yes，那我们就是不是很确定了，那么该物品很可能在集合中（但也存在误伤的概率，错误判断未曝光物品为已曝光，将其过滤掉）。总结一下…

暂时不更新Bloom Filter的内容…

排序

排序01 多目标模型

这节课介绍最基础的多目标排序模型，用在粗排和精排。回顾一下，做完召回之后，要从中选出用户最感兴趣的，这就要用到粗排和精排。粗排给召回的笔记逐一打分，保留分数最高的几百篇，然后用精排模型给这几百篇笔记打分，然后不做截断。几百篇笔记全都带着精排分数进入重排。最后一步时重排，做多样性抽样，并且把相似内容打散，最终有几十篇笔记被选中展示给用户。这节课和后面的课程主要研究粗排和精排，它们的原理基本相同，只是粗排模型小，特征少，效果差一些。粗排的目的是做快速的初步筛选，

排序02 Multi-gate Mixture-of-Experts (MMoE)

排序03 预估分数融合

排序04 视频播放建模

排序05 排序模型的特征

排序06 粗排模型

特征交叉

特征交叉01 Factorized Machine (FM) 因式分解机

特征交叉02 DCN深度交叉网络

特征交叉03 LHUC (PPNet)

特征交叉04 SENet 和 Bilinear 交叉

行为序列

行为序列01 用户历史行为序列建模

行为序列02 DIN模型（注意力机制）

行为序列03 SIM模型（长序列建模）

重排

重排01 物品相似性的度量、提升多样性的方法

重排02 MMR(Maximal Marginal Relevance)多样性算法

重排03 业务规则约束下的多样性算法

重排04 DPP多样性算法（上）

重排05 DPP多样性算法（下）

物品冷启

物品冷启01 优化目标 & 评价指标

物品冷启02 简单的召回通道

物品冷启03 聚类召回

物品冷启04 Look-Alike召回

物品冷启05 流量调控

物品冷启06 冷启的AB测试

涨指标的方法

张指标的方法01 概述

张指标的方法02 召回

张指标的方法03 排序模型

张指标的方法04 多样性

张指标的方法05 特殊用户人群

张指标的方法06 交互行为（关注、转发、评论）